IEEE Trans. Visualization & Comp. Graphics (Proc. InfoVis), 2016
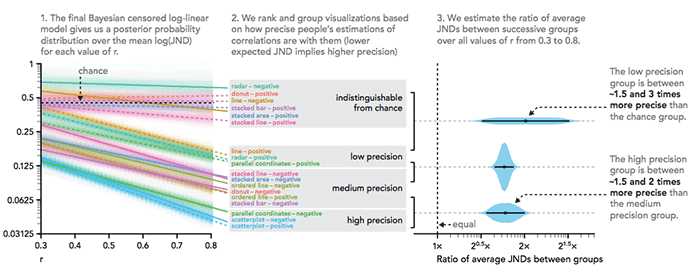
Final model and partial ranking of visualizations. Part 1 may be compared to Figure 6 from Harrison et al. [1], with several notable differences: our results are on a log scale (suggesting a different fit shape), our results provide uncertainty (even if standard errors had been given in Harrison et al. they would not have been valid due to the mean-fitting procedure), and we include all tested visualizations in the analysis. Part 2 may be compared to Figure 7 from Harrison et al., except a total ranking from our results would not be the same (e.g., parallel coordinates–negative and scatterplot–negative swap positions), and we provide and emphasize a partial ranking (instead of a total ranking) consistent with the available evidence. Part 3 has no direct analog in Harrison et al. Posterior densities in Part 3 are augmented with median and 95% quantile credibility intervals.
Abstract
Models of human perception - including perceptual "laws" - can be valuable tools for deriving visualization design recommendations. However, it is important to assess the explanatory power of such models when using them to inform design. We present a secondary analysis of data previously used to rank the effectiveness of bivariate visualizations for assessing correlation (measured with Pearson's r) according to the well-known Weber-Fechner Law. Beginning with the model of Harrison et al. [1], we present a sequence of refinements including incorporation of individual differences, log transformation, censored regression, and adoption of Bayesian statistics. Our model incorporates all observations dropped from the original analysis, including data near ceilings caused by the data collection process and entire visualizations dropped due to large numbers of observations worse than chance. This model deviates from Weber's Law, but provides improved predictive accuracy and generalization. Using Bayesian credibility intervals, we derive a partial ranking that groups visualizations with similar performance, and we give precise estimates of the difference in performance between these groups. We find that compared to other visualizations, scatterplots are unique in combining low variance between individuals and high precision on both positively- and negatively- correlated data. We conclude with a discussion of the value of data sharing and replication, and share implications for modeling similar experimental data.